Tübitak Lise 1. Aşama 1997 Soru 01

[geo]

Kenar uzunluğu $24$ olan bir ABCD karesinin $[AB]$, $[BC]$, $[CD]$ ve $[DA]$ kenarlan üzerinde sırasıyla, $E$, $F$, $G$ ve $H$ noktaları alınıyor. $|DG|=|DH|= 9$ ve $EFGH$ dörtgeni, tabanlarından biri $[HG]$ olan bir yamuk ise, bu yamuğun alanı en çok kaç olur?

$
\textbf{a)}\ 441
\qquad\textbf{b)}\ 306
\qquad\textbf{c)}\ 288
\qquad\textbf{d)}\ 270
\qquad\textbf{e)}\ 225
$

[taftazani44]

|BF|=x diyelim ve (HAE),(EBF),(FCG) üçgenlerinin alanlarının toplamını yazalım ve türevini alalım.
Buradan x=15 olur.
Bu değeri yerine yazarsak istenilen alan 288 olur.

[geo]

Yanıt: $\boxed{C}$

$AC \parallel GH \parallel EF$ olduğu için $BE=BF=x$ tir. $BD \perp AC$ dolayısıyla $BD \perp EF$ ve $BD \perp GH$.

Daha genelini çözmek adına $DH = DG = 9 = y$ ve $AB=24=a$ diyelim.

$GH + EF = (y+x)\sqrt 2$

$BD$, $EF$ ve $GH$ yi sırasıyla $I$ ve $J$ de kessin.

Yamuğun yüksekliği $IJ = BD - BI - DJ = a\sqrt 2 - \dfrac {(y+x)\sqrt 2}2 = \dfrac{(2a-x-y)\sqrt 2} 2$

Yamuğun alanı $$A = \dfrac {(GH + EF)IJ}{2} = \dfrac {(y+x)(2a-x-y)}2 \tag {1}$$
Toplamları $2a = 48$ olan iki sayının çarpımı en fazla $a \times a = 24^2$ olabilir. Bu durumda $\max{A} = \dfrac {a^2}{2} = 288$ dir. $\blacksquare$

Not: $(1)$ de $x+y = z$ dersek else edilen $2.$ dereceden polinomun en büyük değerini parabolün tepe noktasından yola çıkarak ya da polinomun türevini alarak da elde edebiliriz. Bizim çözümde uyguladığımız ise $AO \geq GO$ eşitsizliğinin pratik hali.

[geo]

Daha genelini, yani kenar uzunluğu verilen bir karede $DG = DH$ şartıyla oluşturulan $EFGH$ yamuklarının alanının en fazla karenin alanının yarısına eşit olacağını ispat edeceğiz.

$DH = DG = AE = CF$ olacak şekilde $E,F,G,H$ noktalarını seçelim. Açık şekilde $[EFGH] = \dfrac {[ABCD]}{2}$ dir.

Bunun haricinde şeçilen $E_1, F_1$ noktaları (soldaki şekil) ve $E_2, F_2$ noktaları (sağdaki şekil) için $[E_1F_1GH] < [EFGH]$ ve $[E_2F_2GH] < [EFGH]$ olduğunu göstereceğiz.

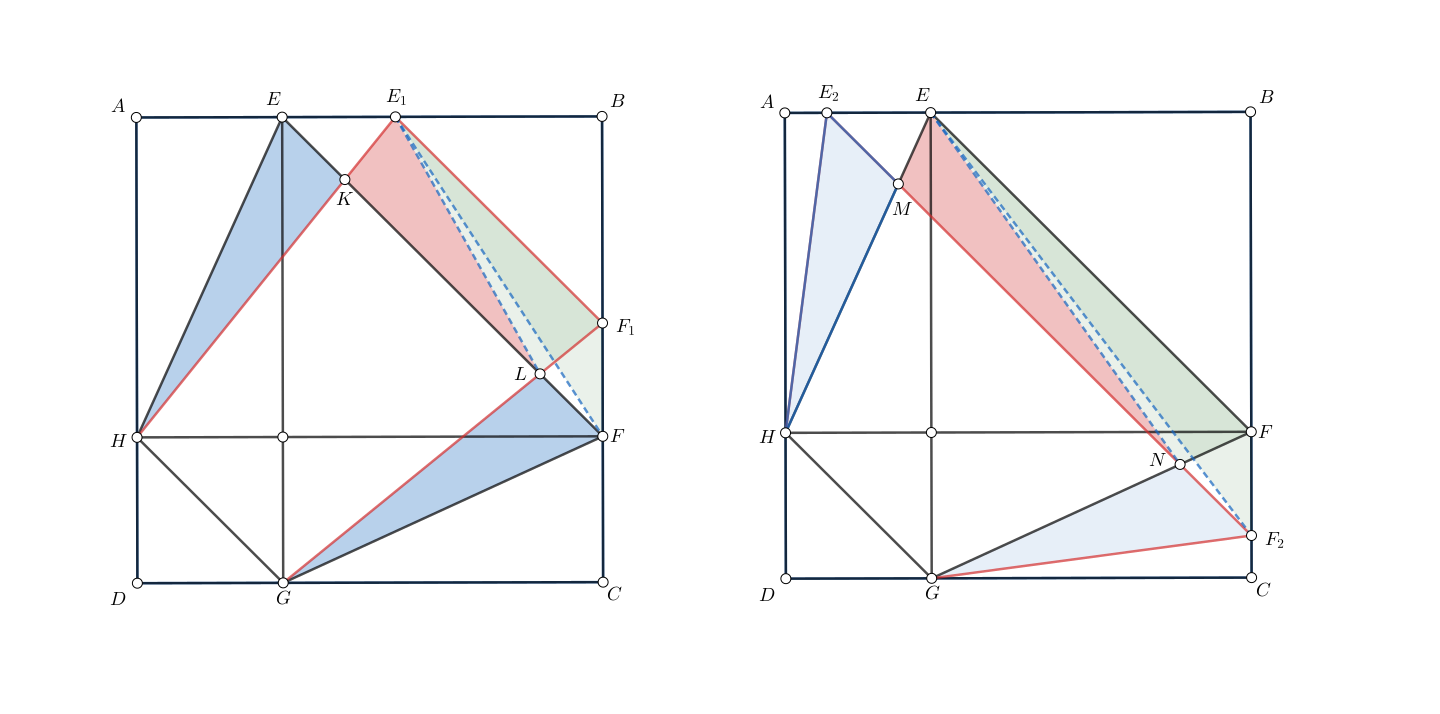
$E_1, F_1$ için (soldaki şekil); $E_1H \cap EF = \{K\}$ ve $F_1G \cap EF = \{L\}$ olsun.
$EFGH$ ve $E_1F_1GH$ yamuklarında $KLGH$ ortak alandır.
$$[EHE_1] = [E_1FE] > [E_1LE] \Longrightarrow [EKH] > [E_1KL] \tag{1}$$
Simetriden dolayı $[EHK] = [FGL]$ ve $[EE_1FH]$ yamuğunda $[EHK] = [E_1FK]$.
$E_1F_1FK$ yamuğunda $KF > E_1F_1$ olduğu için $$[E_1LF_1] < [E_1KF] = [FGL] \tag{2}$$
$(1)$ ile $(2)$ yi birleştirdiğimizde $[EKH] + [FGL] > [E_1LF_1] + [E_1KL] = [E_1L_1FK]$ dolayısıyla $$[EFGH] > [E_1F_1GH] \tag{3}$$ elde ederiz.


$E_2, F_2$ için (sağdaki şekil); $EH \cap E_2F_2 = \{M\}$ ve $FG \cap E_2F_2 = \{N\}$ olsun.
$EFGH$ ve $E_2F_2GH$ yamuklarında $MNGH$ ortak alandır.
$$[E_2HE] < [ENE_2] \Longrightarrow [E_2HM] < [ENM] \tag{4}$$
$$[EFN] = [EFF_2] = [GFF_2] >  [F_2GN] \tag{5}$$
$(4)$ ile $(5)$ birleştirildiğinde $[EFNM] = [EFN] + [ENM] > [E_2HM] + [F_2GN]$ dolayısıyla $$[EFGH] > [E_2F_2GH] \tag{6}$$ elde edilir. $\blacksquare$

[geo]

$AC \parallel GH \parallel EF$ ve $DH=DG$ olduğu için $BE=BF$ ve $EFGH$ ikizkenar yamuktur. Dolayısıyla $FH = EG$.
$EG$ ile $FH$ arasında kalan açı $2\alpha$ olsun. $\angle EGC = 45^\circ + \alpha$ olacaktır.

$AB=a$ dersek, $EG = \dfrac {a}{\sin (45^\circ + \alpha)}$ ve $$[EFGH] = \dfrac 12 \cdot EG \cdot FH \cdot \sin 2\alpha = \dfrac 12 \cdot a^2 \dfrac {\sin 2\alpha}{\sin^2 (45^\circ + \alpha)} \tag {1}$$ olur.

$\sin^2 (45^\circ + \alpha) = (\sin 45^\circ \cos \alpha +\cos 45^\circ \sin \alpha)^2 = \sin^2 45^\circ (\cos\alpha + \sin\alpha)^2 = \dfrac 12 \cdot (1+\sin 2\alpha)$ değerini $(1)$ de yerine yazarsak $$[EFGH] = a^2 \cdot \dfrac {\sin 2\alpha}{1+\sin 2\alpha} = a^2 \cdot \dfrac {1}{ \dfrac {1}{\sin 2\alpha} + 1 } \tag{2}$$ $\max [EFGH]$ için $\sin 2\alpha = 1$ olmalı. Bu durumda $\max [EFGH] = \dfrac {a^2}2$ olur.

[geo]

$D(0,0$, $A(0,24)$, $B(24,24)$, $C(24,0)$ olsun.
$G(9,0)$ ve $H(0,9)$ olacaktır.
$E(x,24)$ dersek $F(24,x)$ olacaktır.
$$[EFGH] =\dfrac 12 \cdot  \begin{vmatrix}
0 & 9 \\
9 & 0 \\
24 & x \\
x & 24 \\
0 & 9

\end{vmatrix} = \dfrac 12 \cdot |9x +24^2+9x-9^2-x^2| =\dfrac{24^2-(x-9)^2}2 \leq \dfrac {24^2}2=288$$