$30$ kişilik bir satranç turnuvasında, şampiyon,  "$3$ kez yenilen elenir" kuralıyla belirlenecektir. Buna göre en az kaç maç yapılmalıdır?

$\textbf{a)}\ 88  \qquad\textbf{b)}\ 87  \qquad\textbf{c)}\ 86  \qquad\textbf{d)}\ 85  \qquad\textbf{e)}\ 84$

$x_1<x_2<x_3<x_4<x_5$ pozitif tam sayılarının ikişer-ikişer toplanmasıyla elde edilen sayı kümesinin $\{18,26,29,34,36,37,44,45,52,55\}$ olduğu bilindiğine göre$,\ x_2$ sayısının rakamlar toplamı kaçtır?

$\textbf{a)}\ 2  \qquad\textbf{b)}\ 5  \qquad\textbf{c)}\ 3  \qquad\textbf{d)}\ 6  \qquad\textbf{e)}\ 4$ 

$OKEK (x,y)+OBEB (x,y)= x+y+4$ denklemini sağlayan kaç tane $(x,y)$ pozitif tam sayı çifti vardır?

$\textbf{a)}\ 0  \qquad\textbf{b)}\ 2  \qquad\textbf{c)}\ 4  \qquad\textbf{d)}\ 6  \qquad\textbf{e)}\ 8$

$f : \mathbb Z \to \mathbb Z$ fonksiyonu her $n \in \mathbb Z$ için

                    $f(f(n+1)-7)=n-1$  ve  $f(f(n))=n$

eşitliklerini sağlıyor. $f(0)=1$ ise $f(2005)$ aşağıdakilerden hangisine eşittir?

$\textbf{a)}\ 7014  \qquad\textbf{b)}\ 7007  \qquad\textbf{c)}\ 7021  \qquad\textbf{d)}\ 7028  \qquad\textbf{e)}\ 7070$

$\dfrac{m(n+3)-1}{m(n+3)+n+2}$ kesri sadeleşecek şekilde kaç tane $(m,n)$ pozitif tam sayı çifti vardır?

$\textbf{a)}\ 0  \qquad\textbf{b)}\ 1  \qquad\textbf{c)}\ 2  \qquad\textbf{d)}\ 4  \qquad\textbf{e)}\ \text{Sonsuz çoklukta}$

$m,n,k$  pozitif tam sayılar olmak üzere$,$

        $\dfrac17 \leq \dfrac{m}{n} < \dfrac13$  ve  $\dfrac{m}{n}=\dfrac{m+k}{nk}$

sağlanacak şekilde kaç tane $\dfrac{m}{n}$ kesri vardır?

$\textbf{a)}\ 5  \qquad\textbf{b)}\ 6  \qquad\textbf{c)}\ 7  \qquad\textbf{d)}\ 8  \qquad\textbf{e)}\ 9$

Alper her gün çekmecesindeki şekerlerin $\dfrac23$'ünün bir fazlasını yiyerek, şekerleri üç günde bitiriyor. Alper'in yemiş olduğu tüm şekerlerin sayısının rakamları toplamı aşağıdakilerden hangisidir?

$\textbf{a)}\ 9  \qquad\textbf{b)}\ 10  \qquad\textbf{c)}\ 11  \qquad\textbf{d)}\ 12  \qquad\textbf{e)}\ 13$

$5$ aynı kalem, $7$ aynı defter ve $9$ aynı silgi iki çocuk arasında kaç farklı şekilde paylaştırılabilir?

Not: Çocuklardan birinin hiçbir şey almadığı durum da sayılacaktır.

$\textbf{a)}\ 2^52^72^9  \qquad\textbf{b)}\ \dbinom52 \dbinom72 \dbinom92  \qquad\textbf{c)}\ \dfrac{21!}{5!7!9!}  \qquad\textbf{d)}\ 315  \qquad\textbf{e)}\ 480$

$5 \leq n \leq 2005$ aralığındaki kaç tane $n$ tam sayısı için

               $n- \bigg[ \dfrac{n}{2} \bigg] = \bigg[ \dfrac{2n}{3} \bigg] - \bigg[ \dfrac{n}{6} \bigg]$

eşitliği sağlanmaz? (Burada, $[a]$ ile $a$ sayısının tam kısmı gösterilmektedir.)

$\textbf{a)}\ 222  \qquad\textbf{b)}\ 266  \qquad\textbf{c)}\ 322  \qquad\textbf{d)}\ 334  \qquad\textbf{e)}\ 366$

$2$'lik sayı tabanına göre yazılışında dört tane $1$ ve altı tane $0$ olan tüm pozitif sayıların toplamını bulunuz.

$\textbf{a)}\ 84(2^9+1)  \qquad\textbf{b)}\ 28(2^{11}-1)  \qquad\textbf{c)}\ 84(2^9-1)  \qquad\textbf{d)}\ 112(2^{10}-1)  \qquad\textbf{e)}\ 14(2^{11}+1)$

$n(n+1)(n+2)...(5n-1)5n$ sayısının $5^{86}$'ya bölünmesini sağlayan en küçük pozitif $n$ tam sayısının rakamları toplamı aşağıdakilerden hangisidir?

$\textbf{a)}\ 13  \qquad\textbf{b)}\ 10  \qquad\textbf{c)}\ 12  \qquad\textbf{d)}\ 14  \qquad\textbf{e)}\ 11$

$ABCD$ dikdörtgeni $[EF]$ doğru parçası boyunca şekildeki gibi katlanmıştır. $|AB|=|AE|=2\ br$ ve $|BF|=1\ br$ olduğuna göre $|B'G|$ kaç birimdir?

$\textbf{a)}\ \sqrt3  \qquad\textbf{b)}\ \dfrac43  \qquad\textbf{c)}\ \dfrac32  \qquad\textbf{d)}\ \dfrac{\sqrt3}{2}  \qquad\textbf{e)}\ \sqrt2+1$

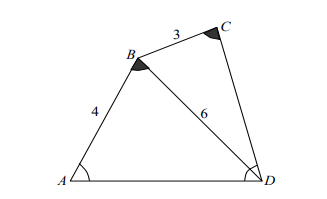Şekilde$,\ |AB|=4\ br,\ |BC|=3\ br,\ |BD|=6\ br,\ m(\widehat{ABD})=m(\widehat{BCD})$ ve $m(\widehat{ADC})=m(\widehat{BAD})$ ise $|DC|$ kaç birimdir?

$\textbf{a)}\ 5  \qquad\textbf{b)}\ 5,2  \qquad\textbf{c)}\ 5,4  \qquad\textbf{d)}\ 6  \qquad\textbf{e)}\ 6,2$

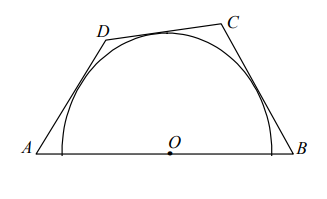Şekildeki $ABCD$ dörtgeninin $AD,\ DC$ ve $CB$ kenarları$,$ merkezi $AB$ parçasının orta noktasında olan çembere teğettir. $|AB|=12\ br,\ |AD|=5\ br$ olduğuna göre $|BC|$ kaç birimdir?

$\textbf{a)}\ 6,2  \qquad\textbf{b)}\ 6,4  \qquad\textbf{c)}\ 7,2  \qquad\textbf{d)}\ 7,4  \qquad\textbf{e)}\ 7,5$

Bir $ABC$ üçgeninde $\widehat A$ açısının açıortayı $BC$ kenarını $D$ noktasında kesiyor.

$|AB|-|BD|=24\ , \quad |AC|+|CD|=54$

olduğuna göre $|AD|$ kaç birimdir?

$\textbf{a)}\ 27  \qquad\textbf{b)}\ 39  \qquad\textbf{c)}\ 32  \qquad\textbf{d)}\ 30  \qquad\textbf{e)}\ 36$

$(x+6)(\sqrt{x+1}-1)^2 \geq x^2$ eşitsizliğini sağlayan $x$ sayılarının bulunduğu en geniş aralığın uzunluğu aşağıdakilerden hangisidir?

$\textbf{a)}\ 3  \qquad\textbf{b)}\ 4  \qquad\textbf{c)}\ 5  \qquad\textbf{d)}\ 6  \qquad\textbf{e)}\ 7$

$5$'in kuvvetleri ve farklı kuvvetlerinin toplamlarından oluşan sayılar artan sırada yazılarak

                     $1,5,6,25,26,30,31,125,...$

dizisi oluşturuluyor. Buna göre bu sayı dizisinin $63$ üncü terimi kaçtır?

$(1=5^0,\ 5=5^1,\ 6=5^0+5^1,\ 25=5^2,\ 26=5^0+5^2,\ 30=5^1+5^2,\ 31=5^0+5^1+5^2,\ 125=5^3\ v.s.)$

$\textbf{a)}\ 3901  \qquad\textbf{b)}\ 3131  \qquad\textbf{c)}\ 3906  \qquad\textbf{d)}\ 3151  \qquad\textbf{e)}\ 775$

$x,y \in \mathbb R$ olmak üzere$,$

$(x-2)(y+2)=(x+y)^2$

eşitliğini sağlayan $(x,y)$ ikililerinin sayısı kaçtır?

$\textbf{a)}\ 1  \qquad\textbf{b)}\ 2  \qquad\textbf{c)}\ 3  \qquad\textbf{d)}\ 4  \qquad\textbf{e)}\ \text{Sonsuz çoklukta}$

$6$ basamaklı pozitif sayılar içinde, $6$ rakamını içeren ve $3$ ile bölünen sayıların sayısına $n$ diyelim. $n$ sayısının $10$ ile bölümünden kalan kaçtır?

$\textbf{a)}\ 2  \qquad\textbf{b)}\ 0  \qquad\textbf{c)}\ 3  \qquad\textbf{d)}\ 8  \qquad\textbf{e)}\ 6$

$X=\{1,2,3,4\}$ kümesi verilsin.

$f:X \to X$ fonksiyonları içinde$,\ a,b,c \in X$ olmak üzere$,\ f(a)=f(b)=f(c)$ koşulunu sağlamayan kaç tane fonksiyon vardır?

$\textbf{a)}\ 200  \qquad\textbf{b)}\ 202  \qquad\textbf{c)}\ 204  \qquad\textbf{d)}\ 208  \qquad\textbf{e)}\ 212$