Geomania.Org Forumları

Problem [Lokman GÖKÇE]: $y' + \dfrac{4}{x}y = \dfrac{4x^2 + 6}{x^3} $ diferansiyel denkleminin $y(2)=3$ koşulunu sağlayan çözümü için $y(1)$ değeri aşağıdakilerden hangisidir?

$\textbf{a) } 20  \qquad \textbf{b) } 21  \qquad\textbf{c) } 22  \qquad\textbf{d) } 23  \qquad\textbf{e) } 24  $





Notlar:

$\bullet$ Malum, soru hırsızlığı konusundan dolayı $2022$ KPSS iptal edildi. Hırsızlara kapıyı içeriden açanların da ortaya çıkarılması dileğiyle, adaylara geçmiş olsun diyorum.

$\bullet$ Matematik ÖABT'ye girecek adaylar için kamuya açık olarak soru-çözüm paylaşarak küçük bir katkı vermiş olalım. Forum içinde başka sorular da paylaşmıştık. Örneğin Bozuk Düzen (Düzensiz Dizilişler) içerikli sorumuz gibi. İyi çalışmalar diliyorum.

Problem (Lokman GÖKÇE): $0\leq n \leq 260$ olmak üzere $n^{12}+n^2-5$ ifadesinin $65$ ile tam bölünebilmesini sağlayan kaç $n$ tam sayısı vardır?


$\textbf{a)}\ 16 \qquad\textbf{b)}\ 20 \qquad\textbf{c)}\ 24 \qquad\textbf{d)}\ 28 \qquad\textbf{e)}\ 32 $

Soru (Lokman GÖKÇE):

$H$ ve $K$, $G$ grubunun iki alt grubu olsun. $|H|=12$ ve $|K|=18$ olduğuna göre, $G$ nin $H \cap K $ alt grubunun mertebesi aşağıdakilerden hangisi olamaz?

$  \textbf{a)}\ 1 \qquad\textbf{b)}\ 2 \qquad\textbf{c)}\ 3 \qquad\textbf{d)}\ 4 \qquad\textbf{e)}\ 6 $

Problem (Lokman Gökçe): $\mathbb{R}^5$ uzayında
\begin{aligned}
W_1 &= \{ (x, y, z, t, v) \in \mathbb{R}^5 \mid x + 2y + 3z - 5t + 2v = 0 \} \,, \\
W_2 &= \{ (x, y, z, t, v) \in \mathbb{R}^5 \mid 2x - y + z + 2t + v = 0 \} \,, \\
W_3 &= \{ (x, y, z, t, v) \in \mathbb{R}^5 \mid -6x + 13y + 7z - 30t + 3v = 0 \}
\end{aligned}

vektör uzayları veriliyor. Bu vektör uzaylarının her birinin alt uzayı olan bir vektör uzayının boyutu en fazla kaç olabilir?

$
\textbf{a)}\ 1
\qquad\textbf{b)}\ 2
\qquad\textbf{c)}\ 3
\qquad\textbf{d)}\ 4
\qquad\textbf{e)}\ 0
$

p:İstanbul'a gideceğim
q:Ankara'ya gideceğim

"İstanbul veya ankara'ya gideceğim. İstanbula'ya gitmeyeceğim. Bu yüzden Ankara'ya gideceğim."

bu argümanda hangi sonuç çıkarma yöntemi kullanılmıştır çözümü nasıldır ?
a)bağlaç  b)modus tollens  c)modus ponens d)kuramsal kıyas  e)ayraç kıyası

Problem: $\displaystyle{\lim_{x\to 0^{-}} \left(x-\dfrac{1}{x}\right)^x}$ limitinin değeri aşağıdakilerden hangisidir?

$  \textbf{a)}\ 0 \qquad\textbf{b)}\ 1 \qquad\textbf{c)}\ e \qquad\textbf{d)}\ +\infty  \qquad\textbf{e)}\ \text{Limit yoktur} $

Soru (Lokman Gökçe): Standart normal dağılıma sahip $Z$ rassal değişkeni için bazı $z$ puanlarına ait $P(Z \leq z)$ olasılık değerleri aşağıdaki tabloda verilmiştir.

$$
\begin{array}{|c|c|}
\hline
z & P(Z \leq z) \\
\hline
0 & 0,5000 \\
\hline
0,5 & 0,6915 \\
\hline
1 & 0,8413 \\
\hline
1,5 & 0,9332 \\
\hline
2 & 0,9772 \\
\hline
2,5 & 0,9938 \\
\hline
3 & 0,9987 \\
\hline
\end{array}
$$

Hilesiz bir zar $720$ kez atılıyor. Üst yüzüne en çok $105$ defa $3$ gelmesi olasılığı aşağıdakilerden hangisine daha yakındır?

$
\textbf{a)}\ 0,0668
\qquad\textbf{b)}\ 0,0968
\qquad\textbf{c)}\ 0,1587
\qquad\textbf{d)}\ 0,1841
\qquad\textbf{e)}\ 0,2119
$

İçi boş bir küpün içine $r$ yarıçaplı dolu bir küre yerleştirelim. Küpü $A$ birimküp su ile doldurduğumuzda küp tamamen dolmuş oluyor. Bu küreyi çıkartıp yerine $r$ yarıçaplı $r$ birim yükseklikte dolu bir silindir koyuyoruz. Kalan kısmı $B$ birimküp suyla dolduruyoruz. Her bir ayrıtı $\dfrac{A}{B}$ birime eşit olan bir $G$ küpü alalım. $G$ küpünün cisim köşegenini $X,Y,Z$ noktaları ile $4$ eşit parçaya ayıralım. $M$ bu küpün köşegen üstüne yer almayan bir köşesi olsun. $|MX|+|MY|+|MZ|$ en az kaçtır? ($\pi=3$ alınız.) (Küpün içinde küre çıkarıldıktan sonra içindeki su boşaltılmıştır.)

$\mathbf{a)}$ ${ 2+\sqrt{13}+\sqrt{29}}$                    $\mathbf{b)}$ ${ 3+2\sqrt{3}+\sqrt{19}}$                    $\mathbf{c)}$ ${ 1+3\sqrt{5}+\sqrt{11}}$                    $\mathbf{d)}$ ${ 7+2\sqrt{10}}$                    $\mathbf{e)}$ $\text{ Hiçbiri}$

Problem (L. Gökçe): $(G,\cdot)$ bir grup ve $x,y \in G$ ise $(y^{-1}xy)^4$ aşağıdakilerden hangisine daima eşittir?

$
\textbf{a)}\ y^{-4}x^4y^4
\qquad{b)}\ y^4x^4y^{-4}
\qquad{c)}\ y^{-4}xy^4
\qquad{d)}\ y^{-1}x^4y
\qquad{e)}\ x^4
$

Problem: $ \displaystyle{ \int_0^{\infty} \dfrac{dx}{x^4 + 4}} $ integralinin değeri aşağıdakilerden hangisidir?

$  \textbf{a)}\ \pi \qquad\textbf{b)}\ \dfrac{\pi}{2} \qquad\textbf{c)}\ \dfrac{\pi}{3} \qquad\textbf{d)}\ \dfrac{\pi}{4}  \qquad\textbf{e)}\ \dfrac{\pi}{8} $

Problem: Analitik düzlemde $y=x+\cos(xy)$ denklemiyle verilen eğrinin $(0,1)$ noktasındaki normal doğrusunun eğimi aşağıdakilerden hangisidir?

$  \textbf{a)}\ 2 \qquad\textbf{b)}\ 1 \qquad\textbf{c)}\ 0 \qquad\textbf{d)}\ -1 \qquad\textbf{e)}\ \text{Tanımsız} $

Soru (L. Gökçe): Enes Öğretmen, öğrencilerine ''$\sin\left(2\pi + \dfrac{\pi}{6}\right)$ ifadesinin değeri kaçtır?'' sorusunu sormuştur. Öğrencilerden biri $\dfrac{1}{2}$ cevabını veriyor. Enes Öğretmen de ''Cevabın doğru. Tahtada çözümünü bize açıklamak ister misin?'' diyor. Öğrenci

$\sin\left(2\pi + \dfrac{\pi}{6}\right) = \sin\left(2\pi \right) + \sin\left(\dfrac{\pi}{6}\right) = 0 + \dfrac{1}{2}= \dfrac{1}{2}$

işlemini yapıyor. Enes Öğretmen, öğrencisinde bir kavram yanılgısı olduğunu düşünüyor. Bunu ortaya çıkarmak için aşağıdaki ifadelerden hangisinin değerini sorması uygun olur?

$
\textbf{a)}\ \sin\left( \dfrac{\pi}{6} - 6\pi \right)
\qquad\textbf{b)}\ \sin\left( \dfrac{\pi}{4} - 2\pi \right)
\qquad\textbf{c)}\ \sin\left( 4\pi + \dfrac{\pi}{4}\right)
$
$
\textbf{d)}\ \sin\left( \dfrac{\pi}{4} + \dfrac{\pi}{4}\right)
\qquad\textbf{e)} $ Öğrenci doğru cevap verdiği için kavram yanılgısı yoktur.

Kutupsal koordinat dönüşümü ile ilgili klasik tarzdaki problemlerden birini sunalım.

Problem:

$$
\int\limits_{0}^{2}\int\limits_{0}^{\sqrt{4-x^2}}(x^2 + y^2)dy \, dx
$$

integralinin değeri aşağıdakilerden hangisidir?

$  \textbf{a)}\ \pi \qquad\textbf{b)}\ \dfrac{3\pi}{2} \qquad\textbf{c)}\ 2\pi \qquad\textbf{d)}\ \dfrac{5\pi}{2}  \qquad\textbf{e)}\ 4\pi $

Problem (L. Gökçe): Analitik düzlemde grafiği verilen eğrinin kutupsal koordinatlarda denklemi aşağıdakilerden hangisi olabilir?


$
\textbf{a)}\ r=\cos(4\theta)
\qquad\textbf{b)}\ r=\cos(2\theta)
\qquad\textbf{c)}\ r=\sin(\theta)
\qquad\textbf{d)}\ r=\sin(2\theta)
\qquad\textbf{e)}\ r=\sin(4\theta)
$

$\sqrt{2013.2014.2015.2016+1}=P$ olmak üzere $P$ nin $\pmod {2017}$ de verdiği kalan kaçtır?

$\mathbf{a)}$ $5$                    $\mathbf{b)}$ ${ 13}$                    $\mathbf{c)}$ ${ 29}$                    $\mathbf{d)}$ ${ 58}$                    $\mathbf{e)}\text{ Hiçbiri}$

Problem (L. Gökçe): Aşağıda verilen eşitliklere göre $\dfrac{\partial f}{\partial y}(2, 1)$ kısmi türevinin değeri kaçtır?

$\begin{array}{lcl}
u(x,y)  & = &  x^2-y^2 \\
v(x,y)  & = &  xy + y^2 + 1 \\
f(x,y) & = & u^2v - 2u+v
\end{array}$

$
\textbf{a)}\ 36
\qquad\textbf{b)}\ 34
\qquad\textbf{c)}\ 32
\qquad\textbf{d)}\ 30
\qquad\textbf{e)}\ 28
$

Uyarı: Bu problem, aşağıdaki 2016-ÖABT matematik lise sınavının 5. sorusunun bir modifiyesidir. Sınavda $f(u,v)=u^2v + u+ v^3$ verilmiştir ancak doğru yazım biçimi $f(x,y)=u^2v + u+ v^3$ olmalıdır. Aksi halde, gerçekten $f(u,v)=u^2v + u+ v^3$ verilmek istendiyse $f(x,y)=x^2y + x+ y^3$ ve $\dfrac{\partial f}{\partial x}=2xy + 1$ olup $\dfrac{\partial f}{\partial x}(1,1)=3$ bulunur. Fakat bu değer seçeneklerde yoktur.

Problem (L. Gökçe): $T: \mathbb R \longrightarrow \mathbb R$, $T(x,y)=(2x+5y, x+3y)$ lineer dönüşümünün  $T^{-1}$ ters dönüşümünün matris gösterimi nedir?

$
\textbf{a)}\ \left[\begin{array}{cc}2&5\\1&3\end{array}\right]
\qquad\textbf{b)}\ \left[\begin{array}{cc}2&1\\5&3\end{array}\right]
\qquad\textbf{c)}\ \left[\begin{array}{cc}3&-1\\-5&2\end{array}\right]
\qquad\textbf{d)}\ \left[\begin{array}{cc}3&-5\\-1&2\end{array}\right]
\qquad\textbf{e)}\ \text{Yoktur}
$

TÜBİTAK tarafından çıkarılan Bilim ve Teknik dergisinin 1998 Ağustos sayısından, Ömer Hayyam ile ilgili bir makale. Yazarı, Deniz Gündüz olarak belirtilmiş. Lise üçüncü sınıfı bitirmiş meraklı bir genç olarak, derginin bu sayısı çıktığı gibi almıştım ben de. Yazıyı pdf dosyası olarak indirebilirsiniz. İyi çalışmalar.

https://youtu.be/h0gbw-Ur_do

$2^n.\sum_{k=0}^{n-1}(-1)^k\cos^n\left(\dfrac{\pi k}{n}\right)=2016$ eşitliği sağlanıyorsa $n$ kaçtır?

$\mathbf{a)}\text{ 63}$                      $\mathbf{b)}\text{ 126}$                      $\mathbf{c)}\text{ 252}$                      $\mathbf{d)}\text{ 504}$                      $\mathbf{e)}\text{ Hiçbiri}$

Soru [Lokman GÖKÇE]: Sierpinski üçgeni şu şekilde oluşturulur.

1. Adım: Bir eşkenar üçgen çiziniz.

2. Adım: Bu eşkenar üçgenin orta noktalarını kullanarak orta kısımda oluşan eşkenar üçgeni maviye boyayınız.

3. Adım: Boyalı olmayan üçgenlere 2. adımdaki işlemi tekrar ve tekrar uygulayınız.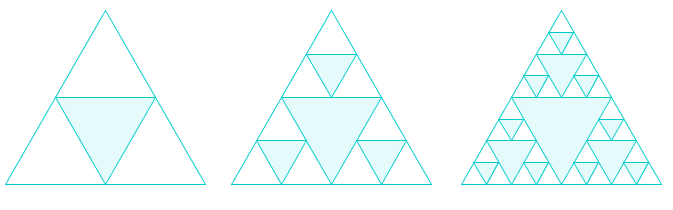



Başlangıç üçgeninin alanı $S$ olsun. Boyama işlemleri $n$ defa uygulandığında, mavi boyalı kısmın toplam alanı $T_n$ olsun. $\displaystyle{\lim_{n\to \infty} \frac{T_n}{S}} $ değeri aşağıdakilerden hangisidir?

$  \textbf{a)}\ \dfrac{3}{4} \qquad\textbf{b)}\ \dfrac{15}{16} \qquad\textbf{c)}\ \dfrac{63}{64} \qquad\textbf{d)}\ \dfrac{255}{256} \qquad\textbf{e)}\ 1 $

Soru (L. Gökçe): $G$ sonlu bir grup olsun. Aşağıdakilerden hangileri doğrudur?

I. $H$, $G$ nin bir alt grubu ise $H$ nın mertebesi, $G$ nin mertebesini böler.

II. Her $a \in G$ için, $a$ nın mertebesi $G$ nin mertebesini böler.

III. $G$ nin mertebesi asal sayı ise, $G$ bir devirli gruptur.

$
\textbf{a)}\ \text{Yalnız I}
\qquad\textbf{b)}\ \text{Yalnız III}
\qquad\textbf{c)}\ \text{II ve III}
\qquad\textbf{d)}\ \text{I ve II}
\qquad\textbf{e)}\ \text{I, II ve III}
$

Problem: $n$ pozitif tam sayılarda değer alan bir değişken ve $k$ pozitif tam sayı olan bir sabit ise
$$  \lim_{n\to \infty} \dfrac{1^k + 2^k + 3^k+ \cdots + n^k}{n^{k+1}}  $$
limiti için aşağıdakilerden hangisi doğrudur?


$\textbf{a)}\ 0 \qquad\textbf{b)}\ \dfrac{k+1}{5k-1} \qquad\textbf{c)}\ \left| \dfrac{k^2-7k}{18k-6} \right| \qquad\textbf{d)}\ \dfrac{1}{k+1} \qquad\textbf{e)}\ \text{Limit yoktur}$



Not: $k$'ya özel değerler vererek seçeneklerden gitmeyi zorlaştırmak için, seçenekler biraz çeldirici olsun istedim.

$2015^{2016^{2016}}+2016^{2015^{2015}}$ ifadesi $\pmod {2017}$ de kaça denktir?

$\mathbf{a)}$ $0$                    $\mathbf{b)}$ ${ 32}$                    $\mathbf{c)}$ ${ 47}$                    $\mathbf{d)}$ ${ 2015}$                    $\mathbf{e)}\text{ Hiçbiri}$

Problem (L. Gökçe): $X=\{ 1,2,3\}$ kümesinin $\varnothing $ dışındaki tüm alt kümelerinin kümesi  $L(X)$ olsun. $L(X)$ kümesi üzerinde $ \beta = \left \{ (A,B): A, B \in L(X) \text {  ve } A \subseteq B \right \}$ kısmi sıralama bağıntısı tanımlanıyor. $\beta$ bağıntısına göre $L(X)$ kümesi ile ilgili olarak aşağıdakilerden hangisi doğrudur?

$\textbf{a)}$ Tam sıralı kümedir.

$\textbf{b)}$ İyi sıralı kümedir.

$\textbf{c)}$ Üç tane minimal eleman vardır ve bunar $\{ 1\}, \{ 2\}, \{ 3\} $ tür.

$\textbf{d)}$ Üç tane maksimal eleman vardır ve bunar $\{ 1, 2\}, \{ 1,3\}, \{ 2,3\} $ tür.

$\textbf{e)}$ En büyük (maksimum) eleman yoktur.

$2013$ yılında yayımlanan Matematik Öğretim Programında bir öğrencinin problem çözme aşamaları aşağıdaki gibi verilmiştir:

1. Problemi Anlama
2. Plan Yapma
3. Planı Uygulama
4. Çözümün Doğruluğunu ve Geçerliğini Kontrol Etme
5. Çözümü Genelleme ve Yeni Problem Kurma

Bu aşamaları gerçekleştirirken yapılan bazı işlemler aşağıda verilmiştir:

a. Verilen resim, şekil, fotoğraf, harita vb. görsellere uygun gerçekçi problem durumları oluşturma
b. Problemin çözümünden yola çıkarak benzer başka problemlerin çözümü için fikir ve stratejiler üretme
c. Problemi başka bir biçimde ifade etme, problemi basitleştirme
d. Belirlenen bir stratejinin gerektirdiği sayısal işlem ve algoritmaları yürütme

Buna göre bu işlemlerle işlemin yapıldığı problem çözme aşamaları eşleştirilirse hangi aşama boş kalır?

$\mathbf{a)}\text{ 1.}$                                    $\mathbf{b)}\text{ 2.}$                                    $\mathbf{c)}\text{ 3.}$                                    $\mathbf{d)}\text{ 4.}$                                    $\mathbf{e)}\text{ 5.}$

Problem (L. Gökçe): $5$ farklı renkte bilye Ali, Betül, Ceyda arasında her biri en az bir bilye alacak biçimde dağıtılacaktır. Ali'ye kırmızı renkli bilye verildiğine göre, diğer bilyeler kaç farklı biçimde dağıtılabilir?

$
\textbf{a)}\ 48
\qquad\textbf{b)}\ 49
\qquad\textbf{c)}\ 50
\qquad\textbf{d)}\ 51
\qquad\textbf{e)}\ 52
$

Problem (L. Gökçe): $S_9$ simetrik grubunda uzunluğu $3$ olan üç ayrık devrin çarpımı biçiminde yazılabilen kaç farklı fonksiyon vardır? (Yani $f=(abc)(def)(ghi)$ biçiminde ve $f \in S_9$ olmalıdır.)

$
\textbf{a)}\ 2240
\qquad\textbf{b)}\ 1680
\qquad\textbf{c)}\ 840
\qquad\textbf{d)}\ 560
\qquad\textbf{e)}\ 280
$

Wolfram alpha sitesi yardımıyla üçgen çizebiliyoruz. Kenarları $48,27,35$ olan bir üçgen ile ilgili alan, çevre, iç açılar ve grafik bilgilerine ulaşmak mümkündür. Ayrıca $a=4,b=3$ yarı eksenlerine sahip güzel bir elips çizmek de mümkündür. Ben bunun içine bir de $r=3$ yarıçaplı çember yerleştirdim.

Soru [Lokman Gökçe]: $a,b,c$ pozitif gerçel sayılar olmak üzere analitik düzlemde bir çember $ax-by=0$ doğrusuna teğettir çember ve $x$ eksenine de $T(c,0)$ noktasında teğettir. Çemberin yarıçapının alabileceği değerler çarpımı, aşağıdakilerden hangisine daima eşittir?

$  \textbf{a)}\ a^2 + b^2 \qquad\textbf{b)}\ c^2 \qquad\textbf{c)}\ \dfrac{c^2a^2}{b^2} \qquad\textbf{d)}\ \dfrac{c^2b^2}{a^2} \qquad\textbf{e)}\ \dfrac{a^2 + b^2}{c^2} $

Sosyal medya hesabıma gelen ve içinden çıkılamadığı belirtilen bir soru şuydu:

 

$\color{red}{\text{Soru:}}$ $f: \mathbb R \to  \mathbb R $, $f(x) = \left( -\dfrac{1}{3}\right)^{2x}$ üstel fonksiyon mudur? Alterne midir?

 

$\color{red}{\text{Cevap:}}$ $x=\dfrac{1}{4}$ için görüntüyü hesaplayalım. $f\left( \dfrac{1}{4} \right)= \left( -\dfrac{1}{3} \right)^{\frac{1}{2}} \not\in \mathbb R$ olduğundan bu şekilde verilen $f$ ifadesi bir fonksiyon değildir. Üstel fonksiyon hiç değildir.

 

Alterne kavramı, ardışık terimleri farklı işaretlere sahip olan diziler için kullanılır. Diziler ise; tanım kümesi doğal sayılar veya doğal sayıların bir alt kümesi olacak biçimde tanımlanan özel fonksiyonlardır. Genel terimi $a(n)$ olan bir dizide, dizinin değişkeni olan $n$'ye $\dfrac{1}{2}, \dfrac{1}{4}, \sqrt{2}, \pi\, \dots $ vb değerler verilmez. $n$; $0, 1, 2, 3, \dots $ gibi doğal sayı değerlerini alabilir ve alterne (İng: alternating) yani dönüşümlü olup olmadığı sorulabilir. Tanım kümesi $\mathbb R $ olan bir fonksiyon için alterne olma kavramı anlamlı değildir. Çünkü, gerçel sayılarda ardışıklık kavramı yoktur. "$\dfrac{1}{2}$ den sonra gelen ilk gerçel sayı nedir?" ya da "$\pi$ den sonra gelen ilk (en küçük) gerçel sayı nedir?" gibi sorular anlamsızdır. Zira, böyle ilk (en küçük) sayıların olmadığını iyi biliyoruz. Çelişki yöntemiyle ispatlanabilir.

 

 

Sorulara cevap verdik. Bu noktada soruda kafa karıştırıcı noktanın ne olduğunu da düşündüm. Şu ek soruyu sorup yanıtlayalım.

$\color{red}{\text{Ek Soru:}}$ $g: \mathbb R \to  \mathbb R $, $g(x) = \left[\left( -\dfrac{1}{3}\right)^{2}\right]^x$ üstel fonksiyon mudur?

$\color{red}{\text{Cevap:}}$ $g(x) = \left[\left( -\dfrac{1}{3}\right)^{2}\right]^x = \left(\dfrac{1}{9}\right)^{x}$ yazılabildiğinden $g$ üstel fonksiyondur.

 

Eğer $g$'de yapılan işlem, $f$'de de yapıldıysa, yanlış yapılmış olur. Şu teoreme bakalım:

 

$\color{red}{\text{Teorem:}}$ $a, b, c \in \mathbb R$ ve $a>0$ olmak üzere $(a^b)^c = (a^c)^b = a^{bc}$ dir.

 

Bu teorem, her $a$ geçel sayısı için yazılmış değildir. Teorem, $a>0$ iken bu eşitliklerin doğru olduğunu söylüyor. $a\leq 0$ için eşitlikler doğru olmayabilir. Hatta $(a^b)^c$, $(a^c)^b$, $a^{bc}$ ifadeleri tanımlı bile olmayabilir. Eğer bu teorem $f$ için de kullanılmaya çalışılırsa çelişkili durumlar oluşur.

 

$\color{blue}{\text{Not:}}$ Soru ile ilgili benim değerlendirmelerim bunlardır. Eklemek istediğiniz kısımlar varsa paylaşabilirsiniz.

Problem (L. Gökçe):

$x,y,z \in \mathbb Z$ olmak üzere, aşağıdaki sayılardan hangisi $x^2 + y^2 + z^2$ biçiminde yazılamaz?

$
\textbf{a)}\ 3405
\qquad\textbf{b)}\ 4109
\qquad\textbf{c)}\ 4242
\qquad\textbf{d)}\ 4727
\qquad\textbf{e)}\ 5323
$

Problem: Bir üçgenin kenarını çap olarak kabul eden üç çember çiziliyor. Bu çemberlerin kuvvet merkezi, üçgenin hangi özel noktasıdır?

$  \textbf{a)}\ \text{İç teğet çemberin merkezi} \qquad\textbf{b)}\ \text{Çevrel çemberin merkezi} \qquad\textbf{c)}\ \text{Ağırlık Merkezi} \qquad\textbf{d)}\ \text{Diklik Merkezi} \qquad\textbf{e)}\ \text{Fermat Noktası} $

Problem (L. Gökçe): $F(x,y)=xy - 3x +4y +7 $ fonksiyonunun $$ B = \{ (x,y) \in \mathbb R^2 | \quad -6\leq x \leq 3, \quad -3 \leq y \leq 4 \} $$ bölgesi üzerindeki en büyük değeri $a$, en küçük değeri $b$ olduğuna göre $a-b$ farkı aşağıdakilerden hangisidir?

$\textbf{a)}\ 50\qquad\textbf{b)}\ 54  \qquad\textbf{c)}\ 57 \qquad\textbf{d)}\ 61 \qquad\textbf{e)}\ 62 $

Benzer bir başlık açılmış mıydı, bilemedim.

Basit bir google aramasıyla aşağıdaki kaynağı buldum:
http://matematik1.com/pages/23/Y01.pdf

AoPS gibi yabancı siteleri takip etmeyi düşünen arkadaşlar için faydalı olabilir.

$\int_{0}^{\infty} \dfrac{\sin x}{x}\ dx$ değeri aşağıdakilerden hangisine eşittir?

$\mathbf{a)}$ $\dfrac{\pi}{3}$                                            $\mathbf{b)}$ $\dfrac{\pi}{2}$                                                $\mathbf{c)}$ $\dfrac{\pi}{5}$                                         $\mathbf{d)}$ $\dfrac{\pi}{4}$                                          $\mathbf{e)}$ $\pi$