Çokgenin içinde,dışında veya üzerinde alınan P noktası soruları

[AtakanCİCEK]

Bu bölüme trigonometrik ceva veya ek çizimle çözülebilen üçgenin içinde alınan $P$ noktası sorularını  ve ilginç açı sorularını ekleyeceğim. Umarım iyi bir Döküman haline getirebilirim.

$1)$ Bir $ABC$ üçgeninin içinde alınan bir $P$ noktası için $m(\widehat{ABP})=27^{\circ}$ , $m(\widehat{CBP})=57^{\circ}$ , $m(\widehat{BCP})=39^{\circ}$  ve $m(\widehat{ACP})=15^{\circ}$ olarak veriliyor. Buna göre $m(\widehat{BAP})$ değeri kaçtır? (İbrahim Atakan Çiçek)

$2)$ $\mid AB\mid = \mid BC \mid$ ve $m(\widehat{ABC})=84^{\circ}$ olan ikizkenar $ABC$ üçgeninin içinde $m(\widehat{DCA})=30^{\circ}$ ve $m(\widehat{DAC}=12^{\circ}$ olacak şekilde bir $D$ noktası alınıyor. Buna göre $m(\widehat{ADB})$ açısı kaç derecedir? ($2019$ Ulusal Antalya Matematik Olimpiyatı)

$3)$  $ABCDEF$  düzgün altıgen olsun. Altıgen içinde

$$m(\widehat{ABP})=m(\widehat{EFP})=55^{\circ}$$
olacak şekilde bir $P$ noktası alınıyor.  Buna göre $m(BAP)$ açısı kaç derecedir ? ($2018$ Ulusal Antalya Matematik Olimpiyatı)

$4)$ $ABCD$ dışbükey dörtgeninde, $m(\widehat{BAC})=40^{\circ}$ , $m(\widehat{ABD})= m(\widehat{CBD})=20^{\circ}$ ve $m(\widehat{CAD})=100^{\circ}$ olduğuna göre  $m(\widehat{BDC})$ kaçtır? ($2014$ Ulusal Antalya Matematik Olimpiyatı)

$5)$  $ABCD$ dışbükey dörtgeninde $m(\widehat{BAD})=70^{\circ}$ , $m(\widehat{BDA})=52^{\circ}$ ,  $m(\widehat{BCD})=55^{\circ}$ , $m(\widehat{ACD})=29^{\circ}$ , olan dışbükey $ABCD$ dörtgeninde  köşegenlerin kesim noktası $E$ noktası ise  $m(\widehat{AED})$  kaç derecedir ? ($2013$ Ulusal Antalya Matematik Olimpiyatı)

$6)$ İkizkenar $ABC$ üçgeninde $\mid BC \mid = \mid AC \mid $ , $m(\widehat{ACB})=106^{\circ}$, $m(\widehat{PAC})=7^{\circ}$ ve  $m(\widehat{PCA})=23^{\circ}$ olduğuna göre  $m(\widehat{CPB})$ açısı kaç derecedir ? ($1993$ Amerika Matematik Olimpiyatı)

$7)$ Bir  $ABC$ üçgeninde  $m(\widehat{BAC})=40^{\circ}$ ve  $m(\widehat{ABC})=60^{\circ}$ olarak veriliyor.  $D$ ve $E$ sırasıyla , $AC$ ve $AB$  kenarları üzerinde , $m(\widehat{CBD})=40^{\circ}$ ve $m(\widehat{BCE})=70^{\circ}$  olacak şekildeki noktalar olsun. $F$ noktası $BD$ ve $CE$ nin kesişim noktası olduğuna göre,  $AF$  nin $BC$ ye dik olduğunu ispatlayınız.($1998$ Kanada Matematik Olimpiyatı)

$8)$ Bir $ABC$ üçgeninin içinde alınan bir $P$ noktası için  $m(\widehat{ABP})=10^{\circ}$ , $m(\widehat{CBP})=20^{\circ}$ , $m(\widehat{BCP})=30^{\circ}$ , $m(\widehat{PCA})=40^{\circ}$ olduğuna göre $m(\widehat{PCA})$  kaçtır?

$9)$  Bir $ABC$ üçgeninin içinde alınan $E$ noktası ile dışında alınan $D$ noktası için $m(\widehat{BAE})=42^{\circ}$ , $m(\widehat{EAC})=18$ , $m(\widehat{ECA})=48^{\circ}$ , $m(\widehat{ECD})=30^{\circ}$ , $m(\widehat{ABE})=54^{\circ}$ ve  $m(\widehat{EBD})=36^{\circ}$  olduğuna göre $m(\widehat{EDC})$ kaçtır ? (Soru $1$ çözümündeki lemma)

$10)$ Bir $ACD$ üçgeninin içinde $m(\widehat{BAD})=30$ , $\mid BC \mid =\mid DC \mid = \mid DB \mid$ olacak şekilde bir $B$ noktası alınıyor. $\mid AD\mid=8$ , $\mid AB\mid =4 $  olduğuna göre $\mid AC \mid$  kaçtır? ($2018$ Ulusal Antalya Matematik Olimpiyatı)

[Squidward]

$2)$


$m(\widehat{ABD})= \alpha$ denilir ve üçgende $D$ noktasına göre birimle derece olmak üzere trigonometrik ceva teoremi yazılırsa,

$\dfrac{\sin{12}}{\sin{36}} \cdot \dfrac{\sin{\alpha}}{\sin{84-\alpha}} \cdot \dfrac{\sin{18}}{\sin{30}} = 1 $

elde edilir, $\sin{30} = \dfrac{1}{2}$ kullanılır ve yarım açı formüllerinden $\sin{36} = 2\sin{18}\cos{18}$ yazılırsa,

$\dfrac{2\cdot \sin{12} \cdot \sin{\alpha} \cdot \sin{18} }{2\cdot \sin{18} \cdot \cos{18} \cdot \sin{84-\alpha}} = 1$

elde edilir, benzer terimler sadeleştirilir ve bilinmeyenli terimler bir tarafta bırakılırsa,

$\dfrac{\sin{\alpha}}{\sin{84-\alpha}} = \dfrac{\cos{18}}{\sin{12}} $

şimdi $\cos{\theta} = \sin{90 - \theta}$ özdeşliği kullanılırsa,

$\dfrac{\sin{\alpha}}{\sin{84-\alpha}} = \dfrac{\sin{72}}{\sin{12}} $

elde edilir ve $\alpha = 72^{\circ}$ olduğu bulunur, istenilen açı $ADB$ üçgeninde bilinmeyen tek açı olduğundan, $180 - 36 - 72 = 72$ elde edilir.
 

[AtakanCİCEK]

$3)$

 Verilen şekil çizilirse $ \mid  AF \mid = \mid  AB \mid $ ve $m(\widehat{FAB})+2m(\widehat{FPB})=360^{\circ}$ olduğundan dolayı $FPB$

üçgeninin çevrel çemberinin merkezi $A$ noktasıdır.  $FB$ ile $AP$ birleştirilirse  $2.m(\widehat{FBP})=m(\widehat{FAP})=50^{\circ}$ 

olacağından $m(\widehat{BAP})=120^{\circ}-50^{\circ}=70^{\circ}$ olmalıdır.



Edit: Resimdeki gereksiz beyaz boş alanlar kırpıldı. (Lokman GÖKÇE)

[Eray]

model üçgen - P noktası isimli çalışmaya göz atabilirsiniz.

[AtakanCİCEK]

$1)$  Çözüm :  (Behzat Erbıçakçı-İbrahim Atakan Çiçek)

İlk önce $\mid AC \mid $ kenarı kenarlarından biri olan ve $ABC$  üçgenini kapsayan $WAC$ eşkanar üçgenini çizelim.

$m(\widehat{BWC})$ açısını hesaplamaya çalışalım.  Bunun için öncelikle $W$  noktasından $AC$ ye dik çizelim.  $AC$ yi kesen noktaya $H$  , $AB$  yi kesen noktaya $F$ diyelim.

$WFA$ ile  $WFC$ üçgenleri eş olduğundan dolayı $FAC$ ikizkenardır.  Açıları yerleştirelim.  Şimdi ise $F$ den $WC$  ye dik inelim. Bu

nokta $G$ olsun. $FWC$ üçgenini katlayalım. ve dışarıdaki noktaya $Q$ adı verelim.  $FQC$ $(72-72-36)$ üçgeni olduğunu gördük ve

$WFCQ$ nun deltoid olduğuna dikkat edersek $WFQ$ nun eşkenar üçgen olduğunu anlarız.  $Q$ ile $B$ noktalarını birleştirelim.  Şimdi

ise $FBC$ üçgeninin $(12-84-84)$ üçgeni olduğuna dikkat edersek $\mid FC\mid=\mid BC\mid=\mid QC\mid$ olacağından dolayı $FBQ$

üçgeninin çevrel çemberinin merkezi $C$ noktasıdır. Buradan ise $m(\widehat{BQF})=6^{\circ}$. Artık Buradan sonra $WFQ$  eşkenar

üçgenine odaklanalım. $m(\widehat{BFQ})=12^{\circ}$ açısının açıortayını çizelim. $BQ$ yu kestiği noktaya $M$ diyelim.  $

m(\widehat{MWQ})=30^{\circ}$  olmalıdır. çünkü $WFM$ ile $WQM$ üçgenleri eştirler. Daha sonra $FBQ$ üçgenini katlayalım.

Katlanan noktaya  $F'$  noktası adını verelim.  $FF'Q$ üçgeninin $(84-84-12)$ üçgeni olduğu görülebilir. Aynı zamanda $\mid

FQ\mid=\mid F'Q\mid =\mid WQ\mid$ olduğundan dolayı  $FF'W$ üçgeninin çevrel çemberinin merkezi $Q$ noktasıdır. Dolayısıyla

$$\dfrac{m(\widehat{FF'Q})}{2}=m(\widehat{F'WF})=6^{\circ}$$ olmalıdır.


$$2m(\widehat{FF'W})+m(\widehat{WQF})=360^{\circ}$$ olduğu için $m(\widehat{QF'W})=66^{\circ}$ olur.  Şimdi ise $WM$ ile

$F'Q$ doğrularının kesiştiği noktaya $Z$ diyelim. $[FM$ ışını Trigonometrik Ceva Teoremi'nin karşıtı gereği  $F$,$B$ , $Z$ doğrusaldır.


$m(\widehat{F'ZF})=24^{\circ}$ olduğu görülür. Aynı zamanda $m(\widehat{ZWF})=24^{\circ}$ olduğundan dolayı  $F'$ ,$W$ ,$Z$

ve $B$ çemberseldir. O halde $$m(\widehat{F'WB})=m(\widehat{F'MB})=24$$ olduğundan dolayı  $m(\widehat{FWB})=18^{\circ}$

olarak bulunur. Buradan uzun zamandır uğraştığımız $m(\widehat{BWC})=12^{\circ}$ olarak bulunur.


Şimdi ise $PBC$ üçgeninin çevrel çemberinin merkezini $O$ noktası olarak alalım. $BOC$ üçgenini katlayıp yeni üçgeni $BCO'$ şeklinde

yazarsak ve açıları yazarsak $BWO'$ üçgeni $(156-12-12)$ üçgeni olduğundan $\mid OB\mid =\mid BW \mid$ olduğu bulunur. Açıları

yerleştirirsek $WBO$ üçgeni $(6-168-6)$  üçgeni olur.  Şimdi ise biraz eşlik görerek sorumuza yaptığımız çözümü bitirelim. $WBC$

üçgeni ile $COW$ üçgenleri eştir. $\mid OW\mid = \mid BC \mid $ görülebilir.  $AWO$ ile $ACB$ $(K-A-K)$ gereğince eş olduklarından

dolayı  $\mid AB \mid =\mid AO \mid$ buradan ise $ABO$ ikizkenar üçgenine odaklanırsak $m(\widehat{BAP})=24^{\circ}$ olarak bulunur.

Lemma: $W$,$F$ , $F'$ ve $O$  noktalarının çemberseldir.

Bu lemmayı da size bırakıyorum...




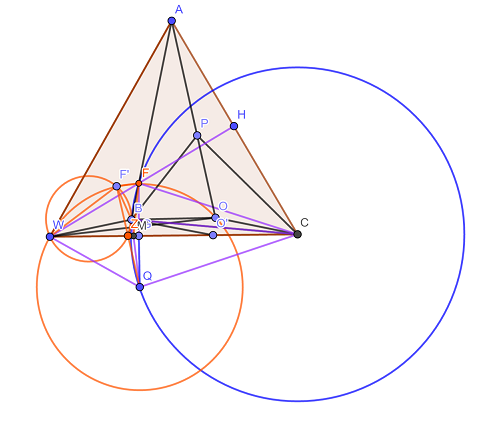Edit: Resim boyutları çok büyüktü, düzenlendi. (Lokman GÖKÇE)

[AtakanCİCEK]

$2)$

Çözüm: (Murat Öz)

$ABE$ şeklinde dışarıdan eşkenar üçgen yapıştıralım. $[EC]$ doğru parçasını çizelim. Soruda Verilen üçgenin ikizkenarlığı ve $ABE$ nin eşkenarlığı ullanırsa $C,D,E$ doğrusallığı görülür. Bundan yararlanılarak diğer açıları da yazar isek $\mid EB \mid= \mid BD \mid$ olduğu görülür. Bu nedenle $\mid AB\mid =\mid BD \mid$  yani  $ABD$ nin $(72-36-72)$ altın üçgeni olduğu görülür.




Çözüm: (Hakan Ulaş)

$BDC$  üçgeninin çevrel çemberinin merkezi $O$ noktası olsun. $2.m(\widehat{BCD})=m(\widehat{BOD})=60^{\circ}$  olduğundan $BOD$  eşkenar üçgen olur. Bilgiler yerleştirilirse  $(K-A-K)$ gereğince $BOC\cong ABC$ olur. Buradan $\mid AB \mid = \mid BD \mid$    yani  $ABD$ nin $(72-36-72)$ altın üçgeni olduğu görülür.



Çözüm: (İbrahim Atakan Çiçek)

Şekildeki gibi bir  $AC// ED $ olacak şekilde doğru çizelim. $ED$ üzerinde $m(\widehat{DBE})=60^{\circ}$ olacak şekilde tek bir nokta olduğunu görebiliriz. Aynı zamanda bu özelliği sağlayan üçgenlerden biri eşkenar üçgen olduğu için $EBD$ eşkenar üçgen olmak zorundadır. Dolayısıyla açımız $60+12=72^{\circ}$ olarak bulunur.

[Squidward]

$4)$ $50$ derecedir.

$AD \parallel BC$'dir, bu yüzden $m(\widehat{ADB})=20^{\circ}$'dir, köşegenlerin kesişim noktasına $K$ dersek, $m(\widehat{DKC})=120^{\circ}$ olduğunu görmek zor değildir, bu sebeple $m(\widehat{BDC})=\alpha^{\circ}$ dersek, $m(\widehat{ACD})=(60-\alpha)^{\circ}$ olur.

Birimler derece olmak üzere dörtgende trigonometrik ceva teoremi yazılırsa,

$\dfrac{\sin{100}}{\sin{40}} \cdot \dfrac{\sin{20}}{\sin{20}} \cdot \dfrac{\sin{100}}{\sin{\alpha}} \cdot \dfrac{\sin{60-\alpha}}{\sin{20}} = 1$

elde edilir, şimdi $\sin{\theta} = \sin{180-\theta}$, $\sin{\theta} = cos(90-\theta)$ özdeşliklerini kullanarak $\sin{100}$'leri çevirip özdeşliği tekrar yazalım.

$\dfrac{\sin{80}}{\sin{40}} \cdot \dfrac{\cos{10}}{\sin{\alpha}} \cdot \dfrac{\sin{60-\alpha}}{\sin{20}} = 1$

şimdi, $\sin{80}$'i ve $\sin{20}$'yi $\sin{2 \theta} = 2 \sin{\theta} \cos{\theta}$ olduğunu kullanarak tekrar yazalım.

$\dfrac{2 \cdot \sin{40} \cdot \cos{40} \cdot \cos{10} \cdot \sin{60-\alpha}}{\sin{40} \cdot \sin{\alpha} \cdot 2 \cdot \sin{10} \cdot \cos{10}} = 1$

şimdi benzer terimleri sadeleştirip, $\cos{40} = \sin{50}$ olduğunu kullanıp bilinmeyenleri bir tarafta yazalım.

$\dfrac{\sin{60-\alpha}}{\sin{\alpha}} = \dfrac{\sin{10}}{\sin{50}}$

$\alpha = 50$ bulunur, $m(\widehat{BDC})=50^{\circ}$'dir.

[AtakanCİCEK]

$10)$  Şekildeki gibi $ADJ$ eşkenar üçgenini yapıştıralım.  Açılar yerleştirildiğinde $m(\widehat{CDJ})=m(\widehat{BDA})$ olduğundan dolayı ve eşkenar üçgenlerden gelen $\mid BD \mid = \mid CD \mid$  ve $\mid AD\mid =\mid JD \mid$  olduğundan dolayı $BDA \cong  CDJ$ olduğundan dolayı $m(\widehat{DJC})=30^{\circ}$ yani $m(\widehat{CJA})=90^{\circ}$ ve $\mid JC \mid=4$ ve $ \mid AJ \mid =8$ olduğundan dolayı $\mid AC \mid=4\sqrt{5}$ olarak bulunur.