Tübitak Avrupa Kızlar Takım Seçme 2019 Soru 5

[Arman]

Dar açılı bir $ABC$ üçgeninde $|BC|$ nin orta noktası $D$ olmak üzere $|AD|$ üzerinde bir $P$ noktası alınıyor. $ABP$ ve $ACP$ açılarının iç açıortayları $Q$ noktasında kesişiyor. $BQ\bot QC$ ise, $Q\in [AP]$ olduğunu kanıtlayınız.

[nk6]

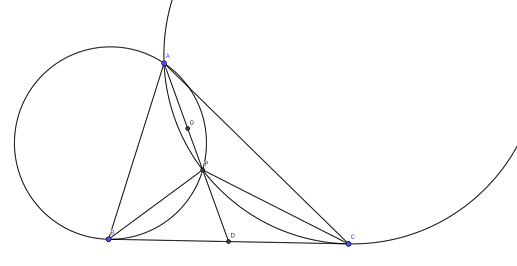
$A$ dan geçen ve $BC$ ye $B$ ve $C$ de teğet olan çemberler $P'$ noktasında kesişsin.

Lemma: $AP$ doğrusu $BC$ yi ortalar (yani $A$, $P$, $D$ doğrusaldır).

İspat: $AP$ doğrusunun $BC$ yi kestiği noktaya $D'$ dersek kuvvetten $|D'B|^2 = |D'P|\cdot|D'A| = |D'C|^2$ olur, dolayısıyla $D'\equiv D$

İddia 1: $P$ noktası $P'$ ne denk olmak zorundadır.

İspat: $\angle{ABP}=2\alpha$ ve $\angle{ACP}=2\beta$ dersek kolaylıkla $\angle{BAC} = 90-\alpha-\beta$ ve $\angle{BPC}=90+\alpha+\beta$ olduğunu buluruz.

Diğer yandan  $\angle{BP'C} = 180-\angle{P'BC}-\angle{P'CB} = 180-\angle{BAC} = \angle{BPC}$ olduğundan ve $AD$ doğru parçası üzerinde bu koşulu sağlayan tek nokta olduğundan $P'\equiv P$ olur.

İddia 2: $\frac{AB}{BP}=\frac{AC}{CP}$

İspat: $ABC$ ve $PBC$ üçgenlerinde sinüs teoreminden:

$\frac{AB}{AC} = \frac{\sin{CAP}}{\sin BAP} = \frac{\sin PCB}{\sin PBC } = \frac{PB}{PC}$

İddia 2'nin soruyu bitirdiği açıktır.

[geo]

$[AD$ üzerinde $AD=DE$ olacak şekilde bir $E$ noktası alalım. $ABEC$ bir paralelkenardır.

$\angle BAC + \angle ABP /2 + \angle ACP/2 = \angle BQC = 90^\circ$

$\angle BPC = \angle BAC + \angle ABP  + \angle ACP=  \angle BAC + (180^\circ - 2 \angle BAC) = 180^\circ - \angle BAC$ olduğu için $BPCE$ bir kirişler dörtgenidir.

$\angle BAE = \angle AEC = \angle PBC$ ve $\angle BEA = \angle PCB$ olacaktır. Bu durumda $\triangle BAE \sim \triangle PBC$ $(AA)$.
Benzerlikten ve paralelkenar özelliklerinden
$$AB/BP = EB/CP=AC/CP$$ elde edilir. Bu da $ABP$ ve $ACP$ açıortaylarının $AP$ üzerinde kesiştiği anlamına gelir. $\blacksquare$